Informatika. Pretvaranje Booleovih izraza

Predloženi će se rad detaljno razmotritipitanje transformacije logičkog izraza. Osim toga, predlažemo vam da poduzmete kratki tečaj o logici, gdje će se ispitati glavni zakoni i koncepti. Preobrazba logičkih izraza je prilično složen proces, ako ne upoznate sve nijanse predmeta.

Tečaj računalne znanosti će se činiti jednostavnim iuživajte ako pažljivo pročitate ovaj članak i upoznate se s pravilima i zakonima preobrazbe, rješavanjem problema i izradom shema. Predlažemo da počnete odmah.

Logika znanosti

Osnove logike - ovo je prilično težak predmet,na njemu je napisano puno svezaka. Ovaj članak će se raspravljati o osnovama zakona transformacije logičkih izraza, to jest, informacija je najviše sažet i koncentriran. To je nužno uzeti u obzir značajnije računalne tehnologije i dizajn kruga.

Za početak, što je logika i zašto je to potrebno? Važno je napomenuti da je to čitava znanost koja razmatra oblike i metode razmišljanja. Sve što vidimo, čujemo ili radimo, poštuje zakone. Bacite loptu s visine - uvijek leti, jer poštuje zakone fizike. Ujutro pripremamo mirisnu kavu, dodamo šećer, a rastrojene tvari odmah rastopiti u vodi, poštujući zakone fizike. Razgovaramo s prijateljima, dijeleći naše planove: "Ako dobro zaštitim posao, dobit ću crveni diplomu", "Ne mogu doći automobilom, jer je pod korakom". Bez primjećivanja, gradimo sve naše razgovore, oslanjajući se na logiku i njegove zakone. Pa zašto nam je potrebna znanost o logici? Naravno, znajući svoje zakone, točno možete odrediti ishod događaja, budući da ne morate djelovati slučajno i riskirati.

Iako je razmišljanje prilično složen proces, ipak se može podijeliti na određene komponente, preciznije oblike (kroz koje se pojavljuje izraz misli):

• koncepti;
• izjave;
• rasuđivanje;
• dokazi.

Zatim predlažemo da idete na logičke funkcije i pretvorite logičke izraze. Informatika će biti zabavna i prilično jednostavna za vas ako pažljivo pročitate ovaj članak.

Logičke funkcije

Sada predlažemo da se upoznamo sa logikomfunkcije. Često, u jedinstvenom državnom pregledu ulaznica u Dijelu B, postoje problemi s preoblikovanjem logičkih izraza u numeričkim segmentima. Ne mogu se riješiti bez poznavanja funkcija logike.

Koji je glavni zadatak ove znanosti? Naravno, proučavanje logičkih izraza (i složenih i jednostavnih). Kako dolazi složena izjava? Spajanjem jednostavnih, što se događa preko paketa, koji se obično nazivaju funkcijama.

Ukupno možete razlikovati pet paketa:

• inversion (to jest, negacija, uz pomoć ove funkcije, može se dobiti izjava, suprotno tome: danas idem u kino - ne idem u kino danas);
• disjunkcija (ta se funkcija često naziva logičnimOsim toga, kako bi se jasno dati jednostavan primjer života: „Ako imam glavobolju ili želudac, onda neću ići u školu” - taj izraz je istina, ako se uzme u obzir barem jedan od zahtjeva);
• zajedno (često se zove logička množenje: "ako pranje posuđa i pouke, onda idem s prijateljima" - taj će izraz biti istinit ako se uzmu u obzir dva uvjeta);
• implikacija (u logici koja se zove ova funkcijaNa žalost, ne može se ilustrirati životna situacija; lažna funkcija će biti u slučaju ako se nešto želi učiniti, ali nije uspjelo, u drugim slučajevima funkcija će biti istinita);
• ekvivalentnost (ili jednakost, ako su dvije izjave istinite ili lažne, onda kao rezultat dobivamo istinu).

Važno je napomenuti da je u računalnoj znanosti bilo jednostavnaizraz je označen velikim slovom latinske abecede. Zatim morate zapamtiti tablicu istine za svaku funkciju. Imajte na umu da nije nužno naučiti, samo će biti dovoljno razumjeti funkcije.

Tablice istine

veznik

razdvajanje

inverzija

Implikacija

Logički jednakosti

Osim toga, to je napomenuti i totfakt koje leže u logici je označen broj 0, a pravi izraz znamenke 1.Radi vaše udobnosti, možete primijeniti i plus i minus znakovi.Obratite pozornost na činjenicu da lažni i istinski izraz predložene tablice su označene s slova "l" i "odnosno.

zgrada

Prije premještanja na transformirati Booleovih izraza, to je potrebno upoznati se sa svojim graditi.Bilo koji spoj ili, kako je rekao prije, složeni izrazod dva dijela:

• varijable koje su označene velikim slovima latinske abecede;
• znakovi koji ukazuju na funkciju i povezivanje jednostavnih izraza.

Kako stvoriti izraz u jeziku algebre logike? učiniti nekoliko stvari:

• Podijelite sve reći jednostavan izraz;
• odrediti te elemente pisma;
• osvijetliti odnos između jednostavnih izraza;
• napisati izraz pomoću posebnih znakova algebre logike.

Ponuda treba uzeti u obzir je jednostavan primjer: (Z * F = 5 ili Z * F = 4), i (Z * F nije jednaka 5, ili Z * F nije jednaka 4).Umjesto toga morate zamijeniti varijable 2. onda se izraz (4 = 5 ili 4 = 4) i (4 se nije jednako 5 ili 4 nije jednako 4).Nakon transakcije, istaknuti izraz i odnose između njih, će se kako slijedi: (F Z) i (Z ili ne (F)).Onda moramo pretvoriti ovaj ulaz, zamjene vrijednosti izjave.Ako je izraz istinit, mora zamijeniti 1, inače 0.Se: G = 1 i 1. nakon potrebne izračune smo dobili rezultat: G = 1, odnosno složeni izraz je istina.

zakoni

Pozivamo vas da razmislite o zakonima logike i pravila za pretvaranje logičkih izraza.To je napomenuti da svaki logički izraz nije pretvaraju u drugi pomoću zakona logike.Sada smo ispitati detaljno sve deset zapovijedi.

Prvi na listi je zakon dvostruke negacije. ", izraz" ne (ne i) ćeJednaki izraz "a".

Komunikativni čin je matematike, sjećati se to vrlo jednostavno.A B = B A * B = B * A.

Sochetatelnyj zakon-(D E) F = (D C) E, isti zakon primjenjuje se na logičko množenje.

Zakon o distribuciji je elementarno otvaranje zagrada. Primjer: (A + B) * C = (A * C) + (B * C).

De Morgan zakon: ne (a b) = NEA * Neuve, ne (je * b) = NEA Neuve, AimplikacijaV = NEA (AimplikacijaV) = u * t.

Idempotence: x x = x ili * =.

Iznimka konstante: 1 = x 1 0 x = x; X * 1 = x, x * 0 = 0.

Sljedeći smo odabrali zakon noncontradiction, ga je slijedio, možete tvrditi sljedeće jednakosti: * new = 0.

U logici su apsorpcija zakon, koji u praksi izgledaKako slijedi: c (c * D) = c i c * (c D) =.

Kao što je važno za pretvaranje logičkih izraza, sjećaš se zakon isključenja: (s * e) (NES * e) = e ili (c e) * (NES e) = e.

Ako pogledate u detalje na i zapamtiti predstavljeni u ovom dijelu zakona, problemi s transformacijom nikada ne događa.Ne manje važno i redoslijed izvršavanja funkcije. platiti više pozornosti na ovu stavku, odgovarajuće alokacije naloga funkcije je ključ za pravilno rješenje problema.

Pravila i zakonitosti transformacija i pojednostavljenje postupka s primjerima

Logički zakoni i pravila za pretvorbu Booleovih izraza se vrlo lako pamte.Ako ste u sumnji za istinitost ni jednog od njih, provjerite sami.Da biste to učinili, morate potrošiti 10 minutsvoego vrijeme i stvaranje tablica za istinitost dobiti odgovor.

Sada nudimo logički zakoni i pravila za pretvorbu Booleovih izraza s konkretnim primjerima.Ovaj će biti osigurali da oba sleduetzakrepit primljenih znanja.Obratiti posebnu pozornost na prioriteti za akciju.

Imamo: p (NES * e). postoji potreba da se pojednostavi izraz: prvo nudimo otkriti zagrade.Onda smo dobili sljedeći izraz: ( NES) * (p e). treba napomenuti odjednom da logička Disjunkcija dvije suprotne izjave dajenas istina. taj se rezultat: 1 * (p e) ponovno otvorene zagrade: (* 1) (1 e).Sada još jednom prisjetiti zakone i dobiti odgovor: c e.

Kao što ste već vidjeli, svi prilično jednostavni. za rješavanje ove zadaće, moraju zapamtiti zakone koji su navedeni u posljednjem odjeljku.Predložiti premjestiti riješiti logičke probleme, jer ovaj posao je već malo više sposoban od prethodne.

Rješavanje problema

Smo upoznali osnove znanosti zove "logika", pretvaranje logičkih izraza smo kratko pregledali, zakoni navedeni.Najteži zadatak u kompilaciju Booleovih izraza je zadatak.To je napomenuti da su mogutreshatsja kroz razmišljanja ili način prevođenja izraz tablice.Ponuditi jedan od njih detaljno pregledati.

Tri dečka (Kiril, Anton i kosta) su u istoj sobi.Odjednom mama iz kuhinje slyshitzvuk slomljena šalice. žure da njegovi sinovi i pitao: "Tko je to učinio?"Otvetbyl sljedeće: Kiril rekao da kupa razbio ne kosti i Anton; Anton kaže da je bio kosta nego Kiril; Kosta tvrdi da krivca ne Anton.Mi smo svjesni da netko je jedan od dečki rekao mama u redu.Trebate saznati koji je razbio pehar.

Logično, reakcija Ćirila i Anton protivorechatdrug drugi, na isti način kao Ćiril s kosti.Stoga, ne oboje mogu biti istinit. učiniti sljedeći zaključak-Anton i kosta rekao istinu a Kiril je začetnik slomljena čaša.Ova metoda primijenjena. Sada pogledajte rješavanje ovaj isti zadatak, samo pomoću transformacije izraza.Za početak ćemo uvesti kratice:

• KR - Ćiril razbija šalicu;
• Kup pobijedio Anton;
• Krivac kosta.

Reakcija dječaka:

• Kirill-vrat
• Anton - NeKR, K;
• Kosta-NEA.

Nudimo da izrazimo, ako KostyaLagao je, a Cyril i Anton su govorili istinu: NK * A = 1 i K * NKR = 1 i A = 1. Pretvarajući izraz, dobivamo kontradikciju: 0 = 1. Naša je pretpostavka pogrešna, vrijedno je provjeriti i druge pretpostavke.

Ako pretpostavimo da je Cyril lagao, i Antoni Kostya je majci rekao istinu, dobili smo sljedeći izraz: K * nonA = 1 i K * NeKR = 1 i nonA = 1. Pojednostavljujući izraz, dobivamo CR * nonA * neK = 1. To sugerira da je naša pretpostavka bila istinita, doista, Cyril je razbio šalicu i lagao majci.

Tablični način rješenja

Razmatrani zakoni logike i transformacijelogički izrazi su nam sigurno pomogli da se nosimo sa zadatkom koji je prikazan u prethodnom dijelu. Sada nudimo tabularnu metodu rješavanja sljedećeg problema.

Dimitri, Anatolij i Ludmila su fanovi poštanski korespondencije, mi znamo da svi živjeliu različitim dijelovima svijeta i imejutraznoe hobi. odrediti tko živiu koji grad i ono što on uživa. sljedeće činjenice:

• Dmitry nikada nije bio u Parizu, a Lyudmila - u Rimu;
• Onaj koji živi u Parizu, kao film;
• čovjek koji živi u Rimu radi vokale;
• Lyudmila averziju prema baletu.

Kako bi riješio problem, trebate napraviti mali stol.

Sljedeći otvas zahtijeva maksimalnu pozornost. sve što ste pročitali u stanju, bi se odraziti na ovaj stol.U toku punjenja u sljedećim stanetjasno:

• Dmitry živi u Rimu i bavi se vokalom;
• Anatoli živi u Parizu i često posjećuju i balet;
• Lyudmila je veliki fan filma, koji živi u SAD-u.

Obratite pozornost da činjenica da je pravi izraz naznačeno znamenka 1 i lažni 0.Popune tablice podataka simbola, da će brzo pronaći otvetna pitanje koje vas zanima.

Mikroshematika

Primjeri pretvaranje logičkih izraza koje smo pogledali su na prvi pogled prilično složen.U jedinstven državni ispit ulaznica stanje mozhetvovse u obliku žetona.

Važno je znati da svi koji se tiče prsta sprava temelji na logičkim elementima, postoje neke uređaje koji obavljajujednu logičku funkciju.

Već smo razgovarali o funkcije poput veznika (logička konjunkcija).To je obično označena simbolom &. ovu funkciju je potrebno za spajanje višestrukih vrijednosti.Na slici vidite logičke sheme.

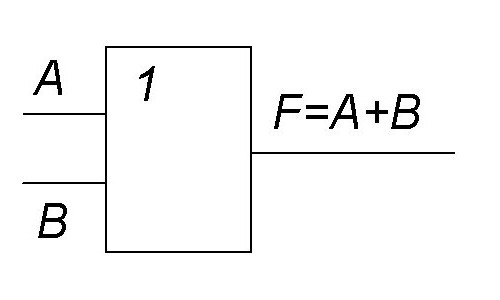
Funkciji provedbe Disjunkcija za Disjunkcija nekih unosa vrijednosti. prilikom pisanja izraza, ova funkcija se zove simbol Ú.Na slici ćete vidjeti shema predstavlja.

Sluzhitpreobrazovatelem inverzija funkcije jednog izraza na suprotnoj slici možete vidjeti kako to izgledashema je "ne".

Primjer za pojednostavljenje formulu # 1

Razmotrena su pravila logičke konverzijeizrazi moraju biti utvrđeni u praksi. Upravo u ostvarenju tog cilja predlažemo da samostalno riješimo dva primjera srednje složenosti i usporedimo ih s rezultatima u ovom dijelu članka.

Nisam zapamtila formule pretvorbe za Booleovih izraza, možemo li se malo "napominalku".Naći ćete da uskoro ti neće biti u mogućnosti miješati u to.

Primjer: (x t) * (NEH t) * (m n). Ne slijepo otpisati, pokušati riješiti, na primjer.

Tijekom pojednostavljivanje, možemo dobiti sljedeće stavke: t * (m ne) = (t * m) (t * ne) = (t *) 0 = (t 0) * (m 0) = t * m.

Kao što možete vidjeti, je prilično dug i nezgrapan složeni izraz imamo k * m.Ako niste uspjeli riješiti primjer, referirati na točke gdje smo vidjeli transformacija logičke izraze, zadaci.

Primjer za pojednostavljenje formulu # 2

U ovom odjeljku predlažemo da pojednostaviteizraz (E + N) * (E + K). Analiziramo rješenje u fazama. Prije svega, moramo otvoriti zagrade, sjetiti se tijeka osnovne matematike. Kao rezultat toga dobivamo sljedeći izraz: E * E + E * K + N * E + N * K. Nadalje, primjećujemo da u rezultirajućem izrazu postoji dio E * E, prisjećamo se zakona idempotencije i pretvorimo zapis: E + E * K + N * E + N * K. Sljedeći korak je transformacija dijela E + E * K, iskorištavanjem uklanjanja varijable E i svojstva: A + 1 = 1. Dobivamo izraz: E + N * E + N * K. Isto tako slijedimo posljednju točku i stavljamo je izvan zagrada E. Kao rezultat, dobivamo odgovor: E + N * K.

Plaća vašu pozornost na činjenicu da posao samo izgleda komplicirano na prvi pogled."Pa ih kao sjeme, samo naučiti osnovne zakone logike.