Sustavi linearnih algebarskih jednadžbi. Homogeni sustavi linearnih algebarskih jednadžbi

U školi, svaki od nas proučavao je jednadžbe i,sigurno, sustav jednadžbi. Ali mnogi ljudi ne znaju da postoji nekoliko načina za njihovo rješavanje. Danas ćemo detaljno razgovarati o svim metodama za rješavanje sustava linearnih algebarskih jednadžbi koje se sastoje od više od dva jednakost.

priča

Do danas poznato je da artriješiti jednadžbe i njihove sustave potječu iz drevnog Babilona i Egipta. Međutim, jednakost u njihovu uobičajenom obliku za nas se pojavila nakon pojave znaka jednakosti "=", koji je 1556. uveo engleski matematičar Record. Usput, taj je znak odabran iz razloga: to znači dva paralelna jednaka segmenta. Doista, najbolji primjer jednakosti ne može se zamisliti.

Utemeljitelj moderne alfabetskiZapis nepoznatog i znakova stupnjeva je francuski matematičar François Viet. Međutim, njezine su oznake bile značajno različite od danas. Na primjer, kvadrat nepoznatog broja označen je slovom Q (lat. "Quadratus"), a kockom slovom C (lat. "Cubus"). Ove oznake sada izgledaju neugodno, ali onda je to bio najčešći način pisanja sustava linearnih algebarskih jednadžbi.

Međutim, nedostatak tada provedenih metodaje da matematičari smatraju samo pozitivne korijene. Možda je to zbog činjenice da negativne vrijednosti nisu imale praktičnu primjenu. U svakom slučaju, talijanski matematičari Niccolo Tartaglia, Gerolamo Cardano i Rafael Bombelli u 16. stoljeću prvi su razmotrili negativne korijene. Moderni oblik, glavna metoda za rješavanje kvadratnih jednadžbi (preko diskriminanta), nastala je samo u 17. stoljeću zahvaljujući Descartesovim i Newtonovim djelima.

Sredinom 18. stoljeća švicarski matematičar GabrielKramer je pronašao novi način da olakša rješavanje sustava linearnih jednadžbi. Ova je metoda naknadno nazvana po njemu i do danas ga koristimo. No razgovarat ćemo o Cramerovoj metodi malo kasnije, ali za sada ćemo raspravljati o linearnim jednadžbama i metodama za njihovo rješavanje odvojeno od sustava.

Linearne jednadžbe

Linearne jednadžbe su najjednostavnije jednadžbe s varijablom (e). Oni su klasificirani kao algebarska. Linearne jednadžbe napisane su u općem obliku kako slijedi: a₁* x₁+ a_{2 *}x₂+ ... a_n* x_nb. Njihova zastupljenost u ovom obliku je potrebna za kompilaciju sustava i matrica dalje.

Sustavi linearnih algebarskih jednadžbi

Definicija ovog pojma je: Ovo je skup jednadžbi koji imaju zajedničke nepoznate količine i zajedničko rješenje. U pravilu, u školi, sve je riješeno sustavima s dvije ili čak tri jednadžbe. Ali postoje sustavi s četiri ili više komponenti. Pogledajmo prvu, kako ih zapisati tako da je u budućnosti bilo prikladno riješiti. Prvo, sustavi linearnih algebarskih jednadžbi izgledat će bolje ako su sve varijable zapisane kao x s odgovarajućim indeksom: 1,2,3 i tako dalje. Drugo, potrebno je sve jednadžbe dovesti u kanonski oblik: a₁* x₁+ a_{2 *}x₂+ ... a_n* x_nb.

Nakon svih tih aktivnosti možemo početi govoriti kako pronaći rješenje sustava linearnih jednadžbi. Mnogo toga za ovo trebamo matrice.

matrica

Matrica je tablica koja se sastoji od žica istupovi, a na njihovom raskrižju su njegovi elementi. To mogu biti specifične vrijednosti ili varijable. Najčešće, za označavanje elemenata, postavljeni su ispod indeksa (na primjer, a₁₁ ili a₂₃). Prvi indeks je redni broj, a drugi je stupac. Preko matrice, kao i preko bilo kojeg drugog matematičkog elementa, moguće je izvršiti različite operacije. Tako možete:

1) Oduzmite i dodajte tablice istih veličina.

2) Pomnožite matricu brojem ili vektorom.

3) Transpose: pretvaranje redaka matrice u stupce i stupce - u redovima.

4) Pomnožite matrice ako je broj redaka jednog od njih jednak broju stupaca druge.

Sve ove tehnike ćemo detaljnije raspravljati, budući da onibit će nam korisno u budućnosti. Oduzimanje i dodavanje matrica je vrlo jednostavan. Budući da uzimamo matrice iste veličine, svaki element jedne tablice korelira sa svakim elementom druge. Tako dodamo (oduzmite) ta dva elementa (važno je da oni stoje na istim mjestima u svojim matricama). Kad množite matricu brojem ili vektorom, jednostavno umnožite svaki element matrice tim brojem (ili vektorom). Prijelaz je vrlo zanimljiv proces. Ponekad je vrlo zanimljivo vidjeti ga u stvarnom životu, na primjer, prilikom mijenjanja orijentacije tableta ili telefona. Ikone na radnoj površini su matrica, a kad se pozicija mijenja, transponirana je i širi, ali se smanjuje u visini.

Analizirat ćemo proces umnožavanja matrica. Iako ne dolazi u uporabu, i dalje će biti korisno to znati. Pomnožite dvije matrice samo ako je broj stupaca jedne tablice jednak broju redaka drugog. Sad uzimamo elemente reda jedne matrice i elemente odgovarajućeg stupca druge. Umnožimo ih jedan drugom, a zatim ih dodamo (to jest, na primjer, proizvod elemenata a₁₁ i a₁₂ na b₁₂ i b₂₂ će biti: a₁₁b₁₂ + a₁₂b₂₂). Dakle, dobivamo jedan element stola i ispunjava se na isti način dalje.

Sada možemo početi razmotriti kako se sustav linearnih jednadžbi rješava.

Gaussova metoda

Ova tema počinje se odvijati u školi. Dobro znamo koncept "sustava dviju linearnih jednadžbi" i možemo ih riješiti. Ali što ako je broj jednadžbi veći od dva? Gaussova metoda će nam pomoći u tome.

Naravno, prikladno je koristiti ovu metodu ako napravimo matricu iz sustava. Ali ga ne možete preobraziti i riješiti ga u čistom obliku.

Dakle, kako se taj sustav može riješiti sustavom linearnogGaussove jednadžbe? Usput, iako je ova metoda nazvana po njemu, ali je otkrivena u davnim vremenima. Gauss sugerira slijedeće: izvršiti operacije s jednadžbama, kako bi na kraju doveli cijeli agregat na oblik sličan korak. To jest, potrebno je da od vrha do dna (ako je pravilno uređeno) od prve jednadžbe do posljednjeg bi se smanjila za jednu nepoznatu. Drugim riječima, trebamo to učiniti tako da dobijemo, recimo, tri jednadžbe: u prvom - tri nepoznata, u drugom - dva, u trećoj - jednini. Tada iz posljednje jednadžbe nalazimo prvi nepoznat, zamjenjujemo njegovu vrijednost u drugoj ili prvoj jednadžbi, a zatim pronađemo preostale dvije varijable.

Cramerova metoda

Za ovladavanje ovom metodom od vitalne je važnostiPosjedujete vještine dodavanja, oduzimanja matrica, a također je nužno biti u stanju pronaći odrednice. Stoga, ako to učinite loše ili ne znate kako, morat ćete naučiti i vježbati.

Koja je suština ove metode i kako to učiniti tako daDobiven je Cramerov sustav linearnih jednadžbi? Vrlo je jednostavno. Moramo izgraditi matricu brojeva (gotovo uvijek) koeficijenata sustava linearnih algebarskih jednadžbi. Da biste to učinili, jednostavno uzeti broj od nepoznatog, a mi dogovoriti stol u redoslijedom kojim su snimljene u sustavu. Ako prije nego što je broj je znak „-”, tada pišemo negativni koeficijent. Dakle, napravili smo prvi matricu koeficijenata nepoznanica, ne uključujući broj nakon znaka jednakosti (naravno, da je jednadžba mora biti sveden na kanonskom obliku, kada je pravo je samo broj, a lijeva - sve nepoznanice s koeficijentima). Tada moramo stvoriti još nekoliko matrica, po jedan za svaku varijablu. U tu svrhu, u prvoj matrici zamjenjuje jedan stupac svaki stupac brojeve s koeficijentima nakon znaka jednakosti. Stoga dobivamo nekoliko matrica, a zatim pronađu njihove determinante.

Nakon što smo pronašli odrednice, slučaj zamali. Imamo početnu matricu, a postoji nekoliko izvedenih matrica koje odgovaraju različitim varijablama. Kako bismo dobili sistemska rješenja, podijelit ćemo determinanta dobivene tablice u odrednicu početne tablice. Rezultantni broj je vrijednost jedne od varijabli. Slično nalazimo i sve nepoznate.

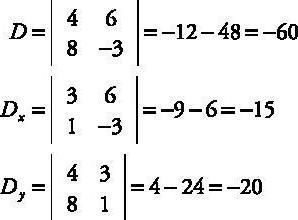
Ostale metode

Postoji nekoliko drugih metoda zaza dobivanje rješenja sustava linearnih jednadžbi. Na primjer, takozvana Gauss-Jordanova metoda, koja se koristi za pronalaženje rješenja za sustav kvadratnih jednadžbi, također je povezana s upotrebom matrica. Tu je i Jacobi metoda za rješavanje sustava linearnih algebarskih jednadžbi. To je najviše prilagodljiva za računalo i koristi se u računalnoj tehnologiji.

Složeni slučajevi

Složenost se obično javlja ako je broj jednadžbimanje od broja varijabli. Tada možemo za neke reći da je bilo sustav nespojivo (to jest, nema korijene) ili broj njegovih rješenja teži beskonačnosti. Ako imamo drugi slučaj, moramo zapisati opće rješenje sustava linearnih jednadžbi. Sadržavat će barem jednu varijablu.

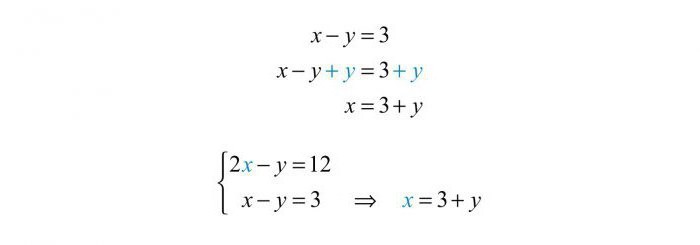
zaključak

Tako smo došli do kraja. Ukratko, analizirali smo sustav i matricu, a naučili smo pronaći opće rješenje sustava linearnih jednadžbi. Osim toga, razmotrili smo i druge opcije. Otkrili su kako je riješen sustav linearnih jednadžbi: Gaussova metoda i Cramerova metoda. Razgovarali smo o kompliciranim slučajevima i drugim načinima pronalaženja rješenja.

Zapravo, ova je tema puno opširnija, a ako želite bolje razumjeti, onda preporučujemo da pročitate više specijalizirane literature.