Kako riješiti jednadžbu ravne linije kroz dvije točke?

Matematika nije dosadna znanost, kao što se ponekad čini. Postoji mnogo zanimljivih, iako ponekad nerazumljivih za one koji to ne žele razumjeti. Danas ćemo razgovarati o jednom od najčešćih i jednostavnih stvari iz matematike, nego da je polje koje je na rubu algebra i geometrija. Razgovarajmo o izravnim i njihovim jednadžbama. Čini se da je to dosadna školska tema, koja obećava ništa zanimljivo i novo. Međutim, to nije tako, au ovom ćemo članku pokušati dokazati našu točku gledišta. Prije nego što idete na najzanimljiviji i opisati jednadžba linije kroz dvije točke, mi gledamo na povijest svih tih mjerenja, a onda saznati zašto je sve to bilo potrebno i zašto sada ne boli znajući sljedeće formule.

priča

Čak iu antičko doba, matematičari su se sviđaligeometrijske konstrukcije i sve vrste grafikona. Danas je teško reći tko je prvi put došao do jednadžbe ravne linije kroz dvije točke. Ali možemo pretpostaviti da je ovaj čovjek Euklid - drevni grčki učenjak i filozof. Bio je on taj koji je u svojoj raspravi "Početak" stvorio temelje buduće euklidske geometrije. Sada se ovaj dio matematike smatra osnovom geometrijskog prikaza svijeta i podučava se u školi. No, treba reći da Euklidska geometrija djeluje samo na makro razini u našem trodimenzionalnom mjerenju. Ako uzmemo u obzir kozmos, nije uvijek moguće predstaviti sve pojave koje se tamo pojavljuju.

Nakon Euclida bili su i drugi znanstvenici. A oni su usavršili i shvatili što je otkrio i napisao. Na kraju se ispostavilo stabilno područje geometrije, u kojoj je sve još uvijek nepogrešivo. I već tisućljećima dokazano je da je jednadžba ravne linije kroz dvije točke vrlo lako sastaviti. Ali prije nego što počnemo objasniti kako to učiniti, raspravljat ćemo o teoriji.

teorija

Crta je beskonačna u oba smjeraSegment koji se može podijeliti na beskonačni broj segmenata bilo koje duljine. Da bi se prikazala ravna crta, najčešće se koriste grafikoni. I grafovi mogu biti u dvodimenzionalnom i trodimenzionalnom koordinatnom sustavu. I oni su izgrađeni prema koordinatama bodova koji pripadaju njima. Uostalom, ako pogledate ravnu liniju, možete vidjeti da se sastoji od beskonačnog skupa bodova.

Međutim, postoji nešto što je linija vrlo jakarazlikuje se od ostalih vrsta linija. Ovo je njezina jednadžba. Općenito, vrlo je jednostavno, za razliku od, recimo, jednadžbe kruga. Sigurno, svatko od nas je prošao u školi. Ali još uvijek napišite njegov opći oblik: y = kx + b. U sljedećem poglavlju ćemo detaljno raspravljati o tome što svako od ovih slova znači i kako riješiti ovu jednostavnu jednadžbu ravne crte koja prolazi kroz dvije točke.

Jednadžba linije

Ravnopravnost koja je prikazana gore, ije nužna jednadžba linije. Vrijedno je objasniti što ovdje znači to. Kao što možete pogoditi, y i x su koordinate svake točke koja pripada ravnoj liniji. Općenito, ova jednadžba postoji samo zato što je za svaku točku bilo koje crte svojstvena povezanost s drugim točkama, pa stoga postoji zakon koji povezuje jednu koordinatu s drugom. Ovaj zakon određuje kako jednadžba ravne linije gleda kroz dvije dane točke.

Zašto dvije točke? Sve je to zato što je minimalni broj točaka potrebnih za izradu ravne linije u dvodimenzionalnom prostoru dva. Ako uzmemo trodimenzionalni prostor, tada će broj bodova potrebnih za izradu jedne pravocrtne linije jednako i dvije, jer tri točke već predstavljaju ravninu.

Tu je i teorem koji dokazuje da je moguće nacrtati jednu ravnu liniju kroz dvije proizvoljne točke. Ta se činjenica može potvrditi u praksi kombiniranjem dviju slučajnih točaka na grafikonu s ravnalom.

Sada razmotrite konkretan primjer i pokazajte kako riješiti ovu zloglasnu jednadžbu ravne linije koja prolazi kroz dvije dane točke.

primjer

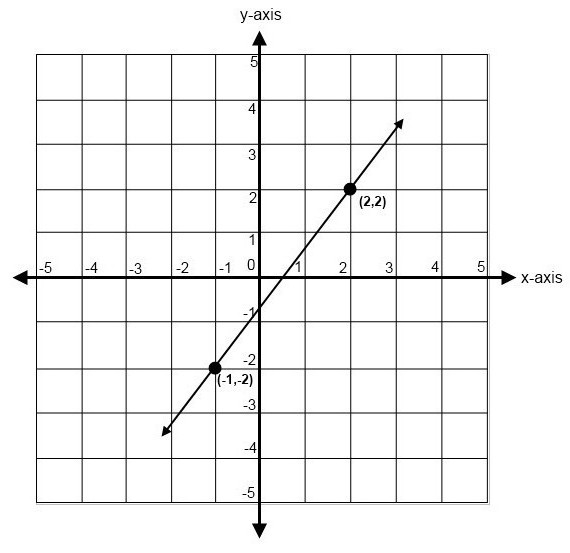
Razmotrite dvije točke kroz koje želite izgraditi pravu liniju. Dajemo im koordinate, na primjer, M₁(2; 1) i M₂(3; 2). Kao što znamo iz tečaja škole, prva koordinata je vrijednost duž OX osi, a druga je duž OY osi. Navedena je jednadžba ravne linije kroz dvije točke, a kako bismo otkrili nedostajuće parametre k i b, moramo sastaviti sustav dviju jednadžbi. Zapravo, to će biti sastavljeno od dvije jednadžbe, od kojih svaka ima dvije naše nepoznate konstante:

1 = 2k + b

2 = 3k + b

Sada ostaje najvažnija stvar: riješiti ovaj sustav. To je učinjeno jednostavno. Prvo, izražavamo iz prve jednadžbe b: b = 1-2k. Sada moramo zamijeniti dobivenu jednadžbu u drugu jednadžbu. To se postiže zamjenom b jednakosti koju smo dobili:

2 = 3k + 1-2k

1 = k;

Sada kada znamo koja je vrijednostkoeficijent k, vrijeme je da otkrijete vrijednost sljedeće konstante - b. Ovo je još lakše. Budući da znamo ovisnost b na k, možemo zamijeniti vrijednost potonjeg u prvu jednadžbu i otkriti nepoznatu vrijednost:

b = 1-2 * 1 = -1.

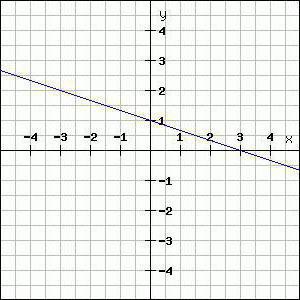
Znajući oba koeficijenata, sada ih možemo zamijenitiu početnu opću jednadžbu ravne linije kroz dvije točke. Dakle, za naš primjer dobili smo sljedeću jednadžbu: y = x-1. Ovo je željena ravnopravnost koju smo trebali dobiti.

Prije nego što krenemo na zaključak, razgovarajmo o primjeni ovog odjeljka matematike u svakodnevnom životu.

primjena

Kao takav, jednadžba ravne linijedvije točke ne nalaze. Ali to ne znači da nam to ne treba. U fizici i matematici vrlo se aktivno koriste jednadžbe linija i svojstava, koje slijede iz njih. Vi to možda niste ni primijetili, ali matematika nas okružuje. Čak i takve naizgled neuhvatljive teme kao jednadžbe ravne linije kroz dvije točke su vrlo korisne i vrlo često primjenjuju na temeljnoj razini. Ako na prvi pogled izgleda da to uopće ne može doći, tada ste pogriješili. Matematika razvija logičko razmišljanje, koje nikada neće biti suvišno.

zaključak

Sada kada smo shvatili kako izgraditi linije na dvije dane točke, ne trebamo odgovoriti na bilo koje pitanje vezano za ovo. Na primjer, ako vas učitelj kaže: "Napišite jednadžbu ravne linije koja prolazi kroz dvije točke ", tada to nećete moći učiniti, nadamo se da vam ovaj članak bude koristan.